Formalizing Correct-by-Construction in Coq

a formalization of CBC Casper using the Coq proof assistant that includes a model of the consensus protocol and proofs of safety and non-triviality protocol properties.

The Correct-by-Construction (CBC) Casper is family of consensus protocol which is partially specified; its specification does not cover synchrony assumptions, liveness, validator rotation, incentive mechanisms, proof-of-stake, light clients, scalability, or message source authentication . In the description of the minimal CBC Casper in , it works with the following five parameters:

  1. Validator names: names of the participants who help to validate and form the consensus
  2. Validator weights: a positive real number assigned to each validator used to measure equivocations of each validator
  3. Byzantine-fault-tolerance threshold: a value strictly smaller than the sum of all the validator weights to denote its tolerance for equivocations
  4. Consensus values: the set of possible decisions which the involved validators jointly make
  5. Estimator: a function which returns a set of possible consensus based on a given protocol state

Note: for a more in-depth context of the background, it is recommended to read: Introducing the ā€œMinimal CBC Casperā€ Family of Consensus Protocols

With these parameters, the Coq proof assistant is used to model the minimal CBC Casper consensus protocol, which is then used to formally verify the desired properties of the protocol: safety and non-triviality. The safety property ensures that when there are not too many equivocating nodes, all participating nodes decide on the same consensus value. The non-triviality property says that it is always possible for participating nodes to make inconsistent decisions on consensus values.

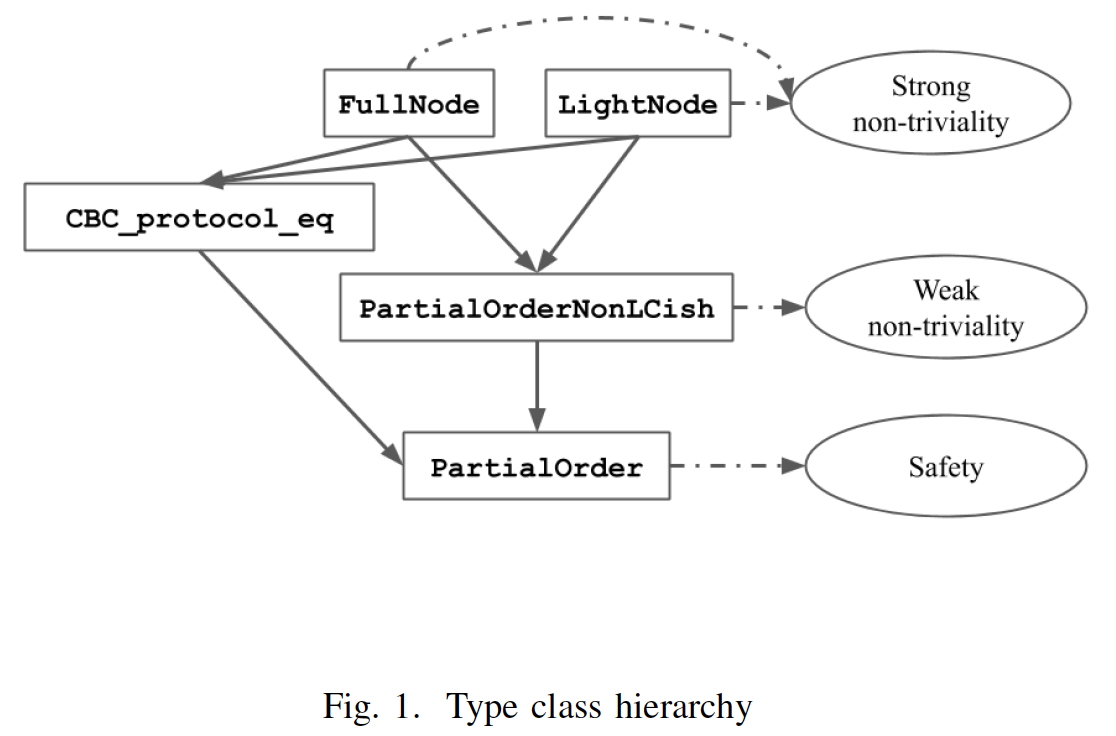
The type classes system in Coq is used to define the abstract hierarchy of the three levels of abstraction: partial order (PartialOrder), partial order with non-local confluence (PartialOrderNonLCish), and a global state transition system (CBC_protocol_eq?).

In Fig. 1 below which was provided in the paper, it depicts the relationships between the three abstractions and the proven properties for each abstraction. From the bottom we have the PartialOrder type class which is sufficient for the safety property to be derived. The PartialOrder type class can then be extended to PartialOrderNonLCish and CBC_protocol_eq type class, with the former exhibiting the weak non-triviality property. Both FullNode and LightNode are two instances of CBC Casper and they have the strong non-triviality property.

Diagram of relationship between the three abstractions and the protocol properties from the paper

Mutual recursion. In this section, they observe that protocol states and messages are mutually and recursively defined on each other. A more detailed explanation of protocol states and messages on their mutual recursion can be found here. The way protocol states and messages are defined presents a challenge on how to model it in Coq. One would consider using mutually defined inductive types to mutually define protocol states and messages; defining equality for them will be tedious. These difficulties are also carried forward to the properties which heavily rely on how our data is defined. An important observation made by the authors of the paper is: the mutual recursive property of protocol states and messages do not contribute to the safety and non-triviality properties and it suffices to represent adding messages to states as a reflexive, transitive reachability relation on states, and how they relate to the protocol states.

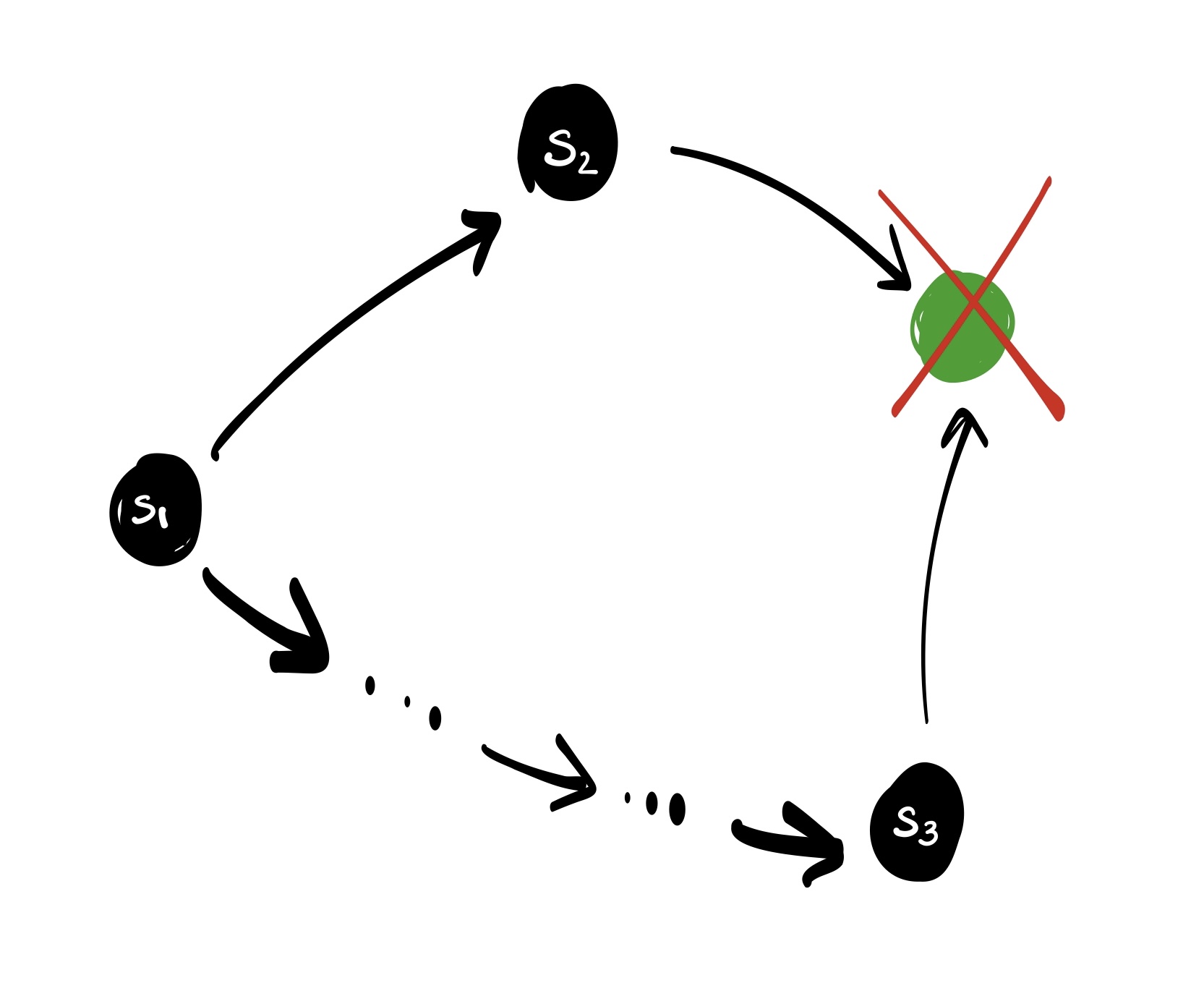
Strong non-triviality. Non-triviality describes the existences of a protocol state that can reach two future protocol states which do not share a common future.

Non-triviality means such a black protocol state exists.

The authors then extends the existential statement of non-triviality to a universal statement: using the reachability relation, for every protocol state \(s_1\), there exists a protocol state \(s_2\) reachable from \(s_1\) in one step and a protocol state \(s_3\) reachable from \(s_1\) in an arbitrary number of steps, such that \(s_1\) and \(s_3\) share a common future, but \(s_2\) and \(s_3\) do not. This stronger property is called strong non-triviality, and can be derived from FullNode and LightNode instances.

The phenomenon above applies to all the protocol states

Safety proof

Within the Protocol.v mentioned in their paper, it presents the safety proof based on the CBC_protocol_eq class:

Theorem n_consistency_consensus `{CBC_protocol_eq} :
  forall ls : list pstate,
    (equivocation_weight (fold_right state_union state0 
    (map (fun ps => proj1_sig ps) ls)) <= proj1_sig t)%R -> 
    consensus_value_consistency ls.

Strong non-triviality proof

As for the proof of strong non-triviality, which is defined as the following,

Definition strong_nontriviality {C V : Type} `{PS : ProtocolState C V} :=
  forall (s1 : pstate C V), exists (s2 : pstate C V), 
    next_future s1 s2 /\ exists (s3 : pstate C V), 
      yes_common_future s1 s3 /\ no_common_future s2 s3.

as shown in Fig 1, this proof of this property are found in their LightNode and FullNode implementations. In their paper, the sketch a constructive proof of strong non-triviality by first introducing the notion of a pivotal node: an additional equivocating node such that the union1 of the resulting two protocol states would exceed the fault weight threshold. Using the existence of such a pivotal node, it is able to construct a pair of equivocating messages for the pivotal node, to construct future nodes such that it satisfies the strong non-triviality illustration shown above.

This concludes the key points of the paper, but there is still more to be understood before we can fully appreciate the specifications of the theorems and properties. We shall now go through type classes formalization found in Protocol.v, and with that prove better clarity as to what is being done in this paper.

Below we have the declarations of the type classes which denote the three different levels of abstractions. The first two classes following the definition of partial order , although it lacks the antisymmetry condition. Following the constructiveness of the Calculus of Inductive Construction type theory implemented in Coq, proof of decidable equality of the data is required and a relation between two elements is implemented as a dependent type instead of a boolean predicate. Extending a partial order to one with non-local confluence, the '{PartialOrder A} is a class constrain - the class PartialOrderNonLCish can only be constructed from a PartialOrder A class.

Partial order type class

Class PartialOrder (A : Type) :=
  { A_eq_dec : forall (a1 a2 : A), {a1 = a2} + {a1 <> a2};
    A_inhabited : exists (a0 : A), True; 
    A_rel : A -> A -> Prop;
    A_rel_refl :> Reflexive A_rel;
    A_rel_trans :> Transitive A_rel;
  }.

Partial order with non-local confluence type class

Class PartialOrderNonLCish (A : Type) `{PartialOrder A} :=
  { no_local_confluence_ish : exists (a a1 a2 : A),
        A_rel a a1 /\ A_rel a a2 /\
        ~ exists (a' : A), A_rel a1 a' /\ A_rel a2 a';
  }.

The third abstraction is one with the least abstractions as it uses the five parameters of a minimal CBC Casper protocol. But as we will realise, the class CBC_protocol_eq contains far more than those five parameters. Subtle but salient details which are used when working proofs on paper and pen are required to be mechanised before they can be used. In the declaration of the validators and consensus values, we them to be StrictlyComparable: an inhabited type with a strictly ordered comparison operator that is reflexive and transitive. For the Byzantine-fault-tolerance threshold (t), the suff_val shows the existence of a list of validators whose sum of weights cross the threshold. This ensures that the fault tolerance threshold is not trivially satisfied. For estimator E which is expressed as a dependent type, we show that the function is total. That is to say, for any state s that is provided to E, there is a consensus value c such that the type E s c is inhabited i.e. the estimator estimates c when given s.

CBC protocol with equality type class

Class CBC_protocol_eq :=
   {
      (** 1 **)
      validators : Type;
      about_validators : StrictlyComparable validators;
      (** 2 **)
      weight : validators -> {r | (r > 0)%R};
      (** 3 **)
      t : {r | (r >= 0)%R};
      suff_val : exists vs, NoDup vs /\ ((fold_right (fun v r => (proj1_sig (weight v) + r)%R) 0%R) vs > (proj1_sig t))%R;
      (** 4 **)
      consensus_values : Type;
      about_consensus_values : StrictlyComparable consensus_values;
      (** 5 **)
      E : state -> consensus_values -> Prop;
      estimator_total : forall s, exists c, E s c;
      
      (** Others **)
      state : Type;
      about_state : StrictlyComparable state;
      state0 : state;
      state_eq : state -> state -> Prop;
      state_union : state -> state -> state;
      state_union_comm : forall s1 s2, state_eq (state_union s1 s2) (state_union s2 s1);

      reach : state -> state -> Prop;
      reach_refl : forall s, reach s s;
      reach_trans : forall s1 s2 s3, reach s1 s2 -> reach s2 s3 -> reach s1 s3;
      reach_union : forall s1 s2, reach s1 (state_union s1 s2);
      reach_morphism : forall s1 s2 s3, reach s1 s2 -> state_eq s2 s3 -> reach s1 s3;

      prot_state : state -> Prop;
      about_state0 : prot_state state0;

      equivocation_weight : state -> R;
      equivocation_weight_compat : forall s1 s2, (equivocation_weight s1 <= equivocation_weight (state_union s2 s1))%R;
      about_prot_state : forall s1 s2, prot_state s1 -> prot_state s2 ->
                                  (equivocation_weight (state_union s1 s2) <= proj1_sig t)%R -> prot_state (state_union s1 s2);
   }.

For the rest of the declarations which is below (** Others **), it specifies four things: state, reach, protocol state and equivocation.

State. The state type is data which StrictlyComparable, with an initial state state0. The state_eq is used to deduce the equality of two states, and two states can be ā€œcombinedā€ together to form another state with the commutative state_union operator.

Reach. The notion of reach is to describe the relation between two states. On top of requiring the reach in a CBC_protocol_eq class to be reflexive and transitive (which is what it means to be StrictlyComparable), it requires a state to reach any state which is a union of itself with another state (reach_union), and the reachability of a state can be extended to other states that are equal to the state which it reaches (reach_morphism).

Protocol state. The prot_state predicate is used to verify when a generic state is a protocol state. For a state to be a protocol state we require the justification of all messages in the state to be a subset of the state for it to be a protocol state (c.f Definition 2.7 ). The about_state0 term verifies that state0 is a protocol state, which will then be used as the preliminary protocol state.

Equivocation. Within the CBC protocol, equivocation_weight computes the sum of the weights of equivocating senders in the given state, and the weight of a state is less than or equal to the weight of a state formed from the union of itself with another state (equivocation_weight_compat). Lastly, it establishes this property (about_prot_state): for any union of two states to be a protocol state, we first need the two states themselves to be protocol states, followed by the equivocation weight of their union to be within the threshold. This is useful as reduces the checking: from checking directly with prot_state on the union to just checking if the equivocation weight of the union is within the threshold.

Conclusion

As we read through the two pages of , there are some things that can be observed. When doing formal verification, one has to be clear on what needs to be verified, and based on it build a formal model and representation that is able to specify the property to be verified. While ideally it is nice to be able to model all aspects of our system, this might not be possible and identifying the crucial properties of the system to model is sufficient. Doing formal verification in Coq allows for the extraction of the formally verified algorithm to Haskell or OCaml that can be used. For this work, while the properties are proven, but is it possible for us to practically extract the algorithms derived from the proofs and directly apply it to use? It seems to make more sense if we are able to make use of the formal verification in the implementation instead of formally verifying it and implementing it separately.

Posted on 18 July 2021

  1. what does it mean by union of protocol states and when do we need to union protocol states together?Ā ↩